início projetos ferramentas

Gilmar Sales

Estudante de Ciências da Computação no Instituto Federal Goiano.

Sparse Sets - Uma Representação Eficiente de Conjuntos Numéricos 03-04-2022

Conjuntos

Conjunto Numérico é uma abstração fundamental bastante utilizada na programação, várias representações são possíveis, cada uma com suas vantagens e desvantagens. Existem duas principais representações amplamente utilizadas: Árvores Binárias e Tabelas Hash

Representações mais comuns

Árvores Binárias de Busca

Esta representação se aproveita da habilidade de inserir elementos ordenados e rotacionar a árvores para mantêlá balanceada para representação conjuntos, e é vantajosa quando o conjunto precisa sempre estar ordenado e possuir muitos elementos.

Tabelas Hash

Esta representação ganha destaque pelo desempenho superior ao das árvores binárias enquanto existirem poucos elementos e por consequência poucas colisões, porém a ordem não pode ser obrigatória.

Tabela de Complexidade Assintótica

Operação Árvore Binária Tabela Hash
Inserir O(lg⁡(n)) o(1); O(n)
Remover O(lg⁡(n)) o(1); O(n)
Pesquisar O(lg⁡(n)) o(1); O(n)
Limpar O(lg⁡(n)) o(1); O(n)
Iterar O(n) O(n)
Espaço O(n) O(n)

Sparse Sets

Sparse Set é uma estrutura de dados simples e muito eficiente que garante um conjunto de números únicos, porém não ordenados. Sua implementação é formada por dois arranjos de números, um esparso (\(S\)) e outro denso (\(D\)), sendo \(|S| + 1\) o valor máximo que pode ser inserido no conjunto, e para que um elemento n exista no conjunto esparso, as seguintes restrições devem ser atendidas:

Restrições

Quantidade

A quantidade máxima de números que podem ser adicionados é igual ao maior número que será inserido mais 1:

\[0 < S[n] < |S|\]

Índice

O índice \(n\) do conjunto esparso aponta para o índice do número \(n\) no conjunto denso:

\[D[S[n]] == n\]

Ex: {5, 1, 4}

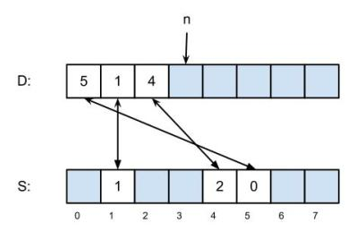
Vantagens

Complexidade Assintótica Superior

Operação Árvore Binária Tabela Hash Sparse Set
Inserir O(lg⁡(n)) o(1); O(n) O(1)
Remover O(lg⁡(n)) o(1); O(n) O(1)
Pesquisar O(lg⁡(n)) o(1); O(n) O(1)
Limpar O(lg⁡(n)) o(1); O(n) O(1)
Iterar O(n) O(n) O(n)
Espaço O(n) O(n) O(n)

Layout de memória

Os números que pertencem ao conjunto são organizados contiguamente no arranjo denso, dando uma vantagem enorme nas operações de inserir, remover, pesquisar e iteração por ter um layout de memória amigável ao cache do processador. Vale lembrar que operações de união, intersecção e diferença são exemplos extremamente relevantes de operações que são implementadas com as operações de inserir, remover, pesquisar e iterar.

Desvantagens

Quantidade finita

As outras representações de conjuntos não possuem a limitação de quantidade existente na definição da estrutura do sparse set, porém ainda são limitadas pelos limites de hardware.

Números negativos

Pela definição da implementação do sparse set ser relativo aos índices, os números negativos não podem ser adicionados nesses conjuntos a menos que: seja delimitado o menor e maior número que pode ser adicionado e com base nisso, os números sejam convertidos para os seus respectivos índices, por exemplo:

Menor: -10, Maior: 100

índice 0 1 2 … 10 … 109
valor -10 -9 -8 … 0 … 100

Glossário

Contiguamente

De modo contíguo, vizinho, próximo, um ao lado do outro.

Por: Gilmar Sales
Particionamento Espacial de Dados 22-11-2021 
#include <iostream>

using namespace std;

/*
 * oaskdoaskd
 */

 class Application
 {
public:
    Application(string name) : m_name(name) {}
    ~Application() = default;

    string get_name() { return m_name; }
private:
    string m_name;
 }

// main function to initialize the application
int main(int argc, char** argv)
{
    Application app = new Application("hello");

    cout << "hello world" << endl;

    return 0;
}
Por: Gilmar Sales
Welcome to Jekyll! 22-11-2021

You’ll find this post in your _posts directory. Go ahead and edit it and re-build the site to see your changes. You can rebuild the site in many different ways, but the most common way is to run jekyll serve, which launches a web server and auto-regenerates your site when a file is updated.

Jekyll requires blog post files to be named according to the following format:

YEAR-MONTH-DAY-title.MARKUP

Where YEAR is a four-digit number, MONTH and DAY are both two-digit numbers, and MARKUP is the file extension representing the format used in the file. After that, include the necessary front matter. Take a look at the source for this post to get an idea about how it works.

Jekyll also offers powerful support for code snippets:

def print_hi(name)
  puts "Hi, #{name}"
end
print_hi('Tom')
#=> prints 'Hi, Tom' to STDOUT.

Check out the Jekyll docs for more info on how to get the most out of Jekyll. File all bugs/feature requests at Jekyll’s GitHub repo. If you have questions, you can ask them on Jekyll Talk.

Por: Gilmar Sales